In Cryptographic, the study of secure communication, where a secretary is absolutely paramount, like for instance, back in the days of roman time, both during the war and other sensitive related subjects. There is a simple cipher named from the time period called Caesar Cipher. This is one of the simplest forms of cipher in Cryptographic, much similar to the XOR cipher in its simplicity.
The Caesar cipher is a symmetric cipher, meaning that both parties require to have the same key, in contrast to the asymmetric cipher where both parties do not use the same key. So let us presume that we have successfully exchanged the key since the whole exchanging of keys is a whole study case on its own.
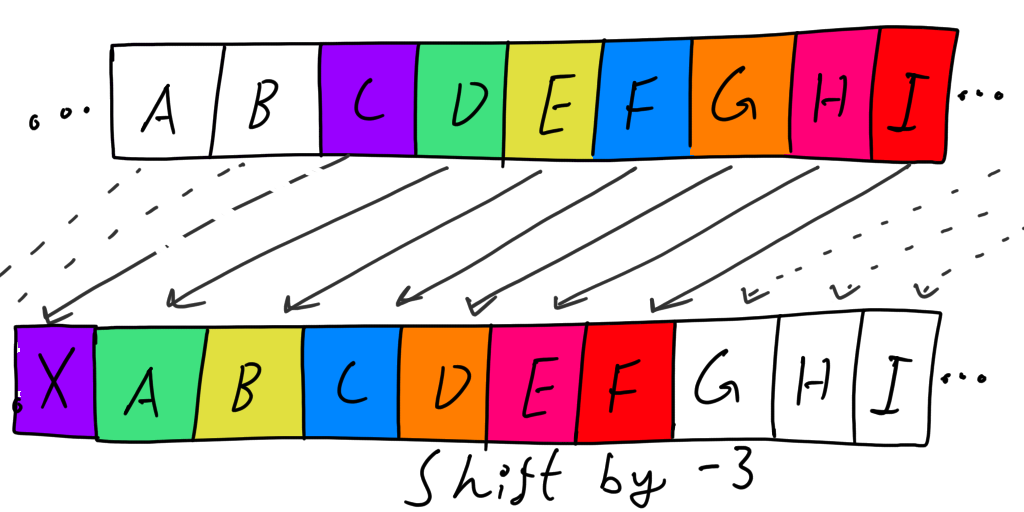
The cipher algorithm is simply shifting all the letters in the text in one direction with a constant offset. For instance, shifting the ‘a’ letter three characters to the right would yield ‘d’, and ‘b’ would yield ‘e’ and etc. Though, when reaching the final character in the alphabet it wraps around. You can either create your own program or use online calculators to try it out in action. See the following section for the equation for the cipher.
The following equations 1 and 2 are the respective encryption and decryption equation for the Caesar cipher. Where ![]() corresponds to plain text, or the non-encrypted, whereas the
corresponds to plain text, or the non-encrypted, whereas the ![]() is the encrypted value.
is the encrypted value. ![]() Finally, the c denotes cardinality of the set of possible numbers. Where the modular denoted as mod will create the wrap-around effect.
Finally, the c denotes cardinality of the set of possible numbers. Where the modular denoted as mod will create the wrap-around effect.
(1) ![]()
(2) ![]()
Examples
Let us take a look at some examples to get an intuitive understanding of what the result will actually look like. For the following example, using the lowercase set, it has the size of 26 possible characters and a shift of 1.
Plain text: hello there, said obi-wan in star wars, revenge of the sith
Ciphertext: ifmmp uifsf, tbje pcj-xbo jo tubs xbst, sfwfohf pg uif tjui
Despite the fact that all letters are only shifted by a single letter to the right in the alphabet. It will at first glance look like a sequence of random characters. However, by looking at the original plain text, we can see patterns, for instance, all of the ‘i’ letter in the plain text is written as ‘j’ in the ciphertext, this will the key component for cracking the key.
Determine the Key – Crack the key
So, let us say we need to decrypt a secret message which we know using the Caesar cipher, how to decrypt it? Both the shift ‘k’ and ‘c’ would need to be determined in order to have successfully obtained the key.
Exhaustive Search
Exhaustive Search is a common technique in cryptography, where you simply try all possible combinations. In this case, assuming that c is 26, using lowercase letters, then checking all possible k values would be required. More precisely, checking it against all elements in the whole number set. The only problem is it could be a very slow process that would take a long time (although, not today, using modern computer power).
Frequency Analysis
If we instead knew that the original text was written in English and have a bigger text for instance. Then using frequency analysis can be done text. Because in the English language, one of the most common words are the, which is three characters long so that if the word in ciphertext for the is uif. That would mean that there is a much higher count than any other words. Thus once determine on a set of highly frequent words, they can be presumed to be one of the more common English words used. Then use an exhaustive search on a small set of words and compare it till any of the decrypted words matches any of the common English. Then it is much more likely the correct key has been found.
Verdict
Should you use Caesar cipher in any of your applications, and the answer is a complete NO! Because if assumed using a single shift value k and constant c, it will yield too much of a pattern which is the last thing that you want in a secure communication protocol. Instead, the more it appears as a sequence of random noise the better.

Free/Open software developer, Linux user, Graphic C/C++ software developer, network & hardware enthusiast.